- This is a summary of Tree Problems in LeetCode. Including the thought, code and some tricks.
Preorder
100. Same Tree
- 可套用模板,双pre
1
2
3
4
5
6public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == null && q == null) return true;
if(p == null || q == null) return false;
if(p.val != q.val) return false;
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
101. Symmetric Tree Preorder
- SameTree拓展
- 判断root的两个子树是不是sameTree
1
2
3
4public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return isSameTree(root.left, root.right);
}
572. SubTree of Another Tree
- SameTree拓展
- 先判断是不是sameTree,然后递归调用一半左一半右
257. Binary Tree Paths
- DFS preOrder模板,判断null返回,判断叶子加上val,每递归一层加上->+val
112. Path Sum + 113. Path Sum II + ==437. Path Sum III==
- PathSum: 双pre,判断叶子,return用or连接左右递归
- PathSumII: 顺序preOrder,==两个递归完成后进行==
list.remove(list.size()-1) - ++PathSumIII: Solution 顺序Pre加上prefixSum的HashMap++
129. Sum Root to Leaf Numbers
- 双pre,左递归+右递归,每一层的值是
10 * x + root.val,遇叶子返回
298. Binary Tree Longest Consecutive Sequence
- 顺序Pre,传参sum,每到一个节点判断val是否连上,连上的话sum++,连不上的话sum=1(重置sum)
- 判断sum之后要进行maxRes操作,取当前最大值作为res (res是全局变量)
111. Minimum of Binary Tree
- 顺序pre,叶子节点更新minRes,参照最大深度的双pre,两种方法都能做
654. Maximum Binary Tree
- DFS,顺序pre,传参start, end,找start,end中的最大值建root,然后顺序递归,左start,max-1,右max+1,end
- BFS, Solution Code-solution),要用Deque做
Postorder
226. Invert Binary Tree (Postorder+BFS)
- BFS,level order traversal,用queue
- DFS, 顺序postOrder,实例化递归返回leftNode和rightNode,中点位置进行对调操作,返回root
104. Maximum Depth of Binary Tree
- DFS, 可以参照111. MinimumDepthOfBT来顺序递归,叶子更新maxRes
- 也可以双post? 不传参的话==return Math.max(helper(root.left), helper(root.right))+1==,传参level的话每次调用level+1,返回左右最大值
110. Balanced Binary Tree
- DFS, 基于MaximumDepth,顺序post,在helper函数中实例left和right的maxDepth,然后root处进行判断,返回的是 ==Math.max(l, r)+1==
116. Populating Next Right Pointers in Each Node
- BFS, LevelOrder
- DFS, preOrder,中节点处操作左右next,
root.right.next = root.next.left
236. Lowest Common Ancestor of Binary Tree
- DFS, 顺序postOrder,终结条件:判断为空或者p q时return root, 实例化左右递归,操作中节点时,进行三重判断
1
2
3
4
5
6
7
8
9
10
11
12public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q)
return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) return root;
else if (left == null) return right;
else return left;
//return left != null && right != null ? root : (left != null ? left : right);
}
124. Binary Tree Maximum Path Sum
- DFS,顺序postOrder,在中节点处维护一个maxRes
- helper函数记录在每个中节点处的1. maxRes 2.返回该节点左右子树的累计最大值加上自己的val
1
2
3
4
5
6
7private int helper(TreeNode root, int[] res){
if (root == null) return 0;
int left = Math.max(0, helper(root.left, res));
int right = Math.max(0, helper(root.right, res));
res[0] = Math.max(res[0], left+right+root.val);
return Math.max(left, right)+root.val;
}
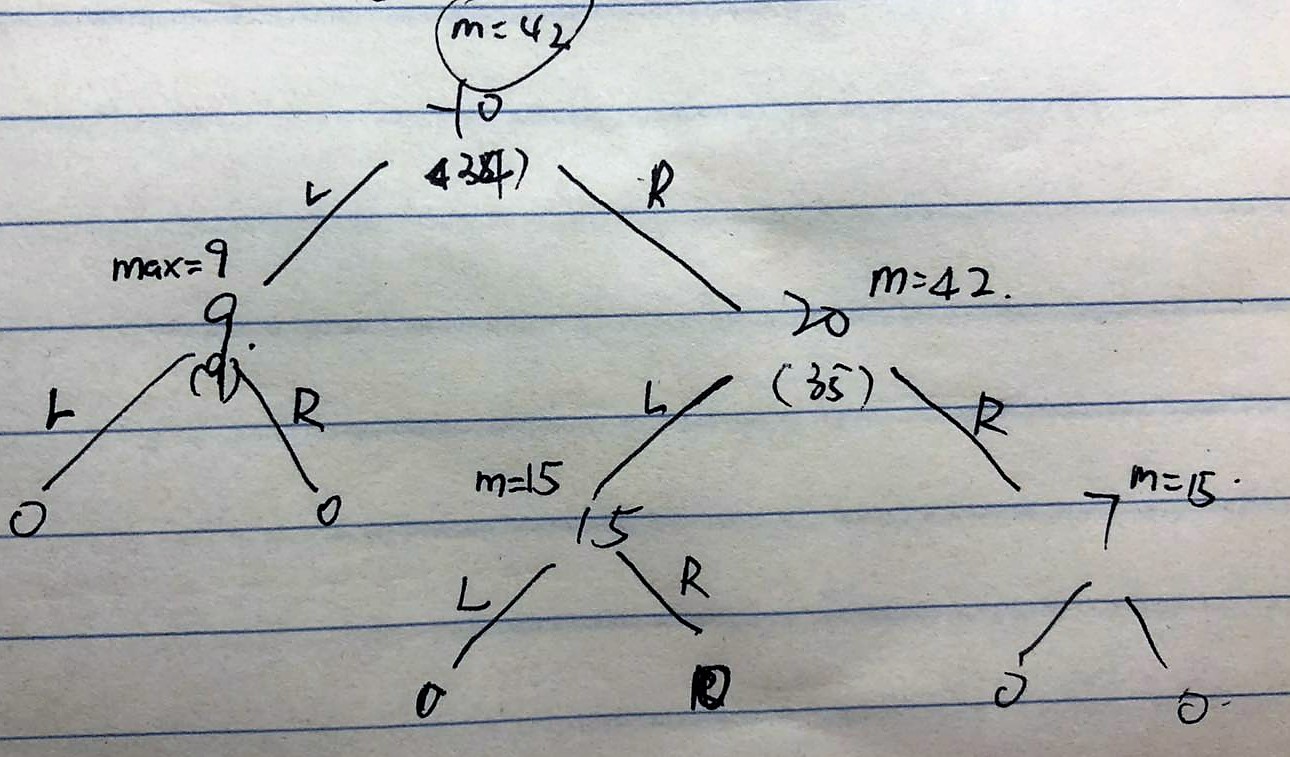
250. Count Univalue Subtrees
- 题意是求多少个相同val的子树,所以要看每个根节点,两种情况1. 左右都null 2. 左右和根节点val相同
- DFS,顺序postOrder,return boolean,传参根节点val,实例化递归左右子树
- 在根节点判断左右Boolean值,返回并判断根节点val和父亲val是否相等
1
2
3
4
5
6
7
8
9
10
11private boolean count(TreeNode root, int[] counter, int val) {
if (root == null) {
return true;
}
boolean l = count(root.left, counter, root.val);
boolean r = count(root.right, counter, root.val);
if (l && r) {
counter[0]++;
}
return l && r && root.val == val;
}
366. Find Leaves of Binary Tree
- 带高度的postOrder 很重要
1
2
3
4
5
6
7
8
9
10
11private int helper(List<List<Integer>> res, TreeNode root){
if (root == null) return -1;
int leftHeight = helper(res, root.left);
int rightHeight = helper(res, root.right);
int rootHeight = Math.max(leftHeight, rightHeight)+1;
if (res.size() == rootHeight) res.add(new ArrayList<>());
res.get(rootHeight).add(root.val);
return rootHeight;
}
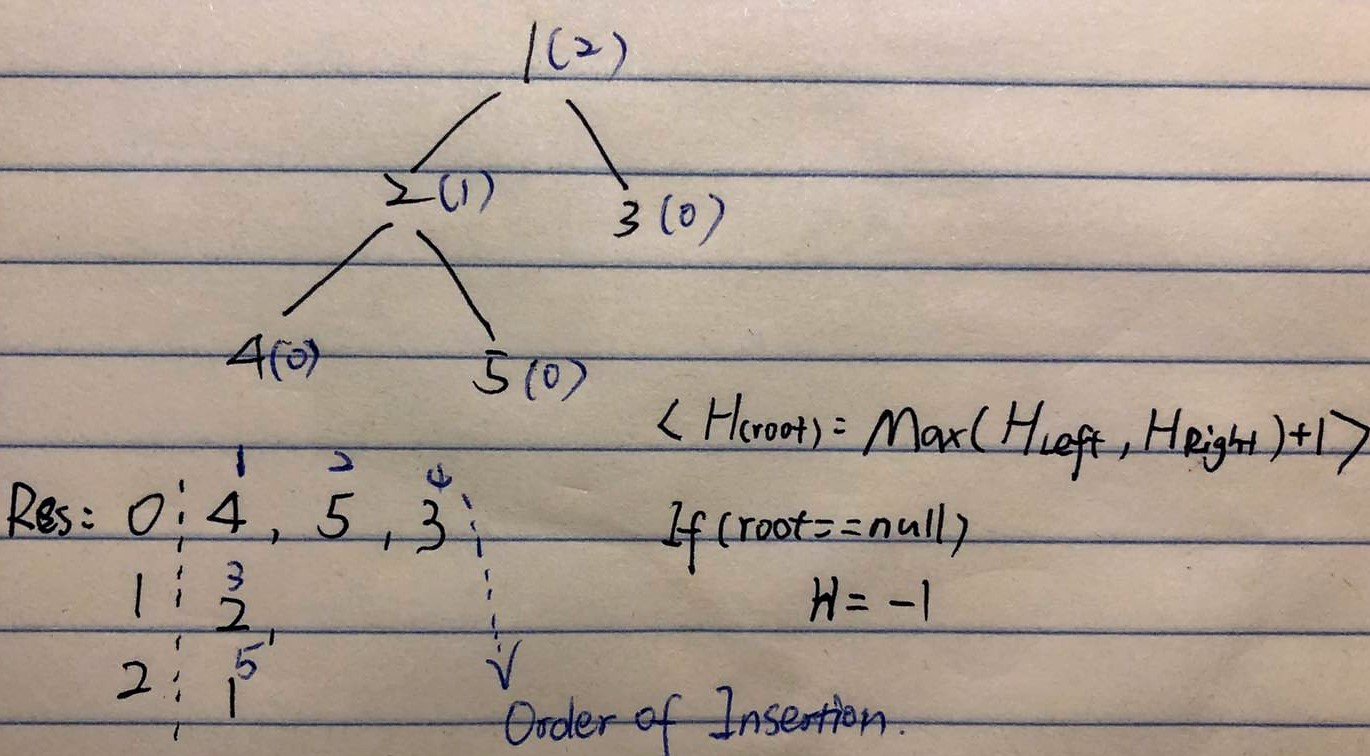
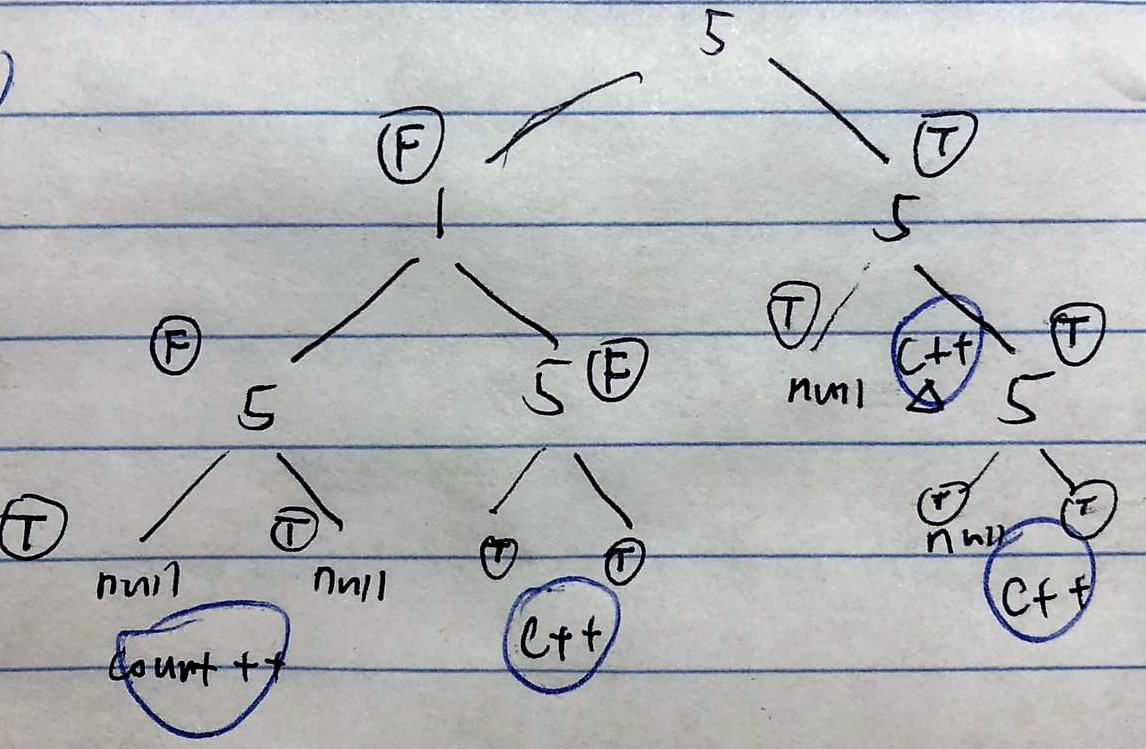
337. House Robber III
- 这是一个分情况返回累加最大值的问题,helper内初始化一个变量,最后返回
- 在左右子树时计算选择隔行的情况,在中节点出计算选择下一行的情况,最后返回较大值
1
2
3
4
5
6
7
8
9
10
11private int helper(TreeNode root){
int left = 0, right = 0;
if (root == null) return 0;
if (root.left != null){
left += helper(root.left.left)+helper(root.left.right);
}
if (root.right != null){
right += helper(root.right.left)+helper(root.right.right);
}
return Math.max(root.val+left+right, helper(root.left)+helper(root.right));
}
BFS
107. Binary Tree Level Order Traversal II
- 考LinkedList的addFirst操作,声明的时候要
LinkedList<List<Integer>> res = new LinkedList<>();
103. Binary Tree Zigzag Level Order Traversal
- Level Order Traversal,加个boolean判断左右
199. Binary Tree Right Side View (BFS+Preorder)
- BFS, 用Queue进行level order tarversal,每当poll出最后一个node时添加到res中
- DFS, preOrder,递增变量是树的
level (start from 0), 每当queue.size() == level时,就添加当前root1
2
3
4
5
6void helper(TreeNode root, List<Integer> res, int level){
if(root == null) return;
if(level == res.size()) res.add(root.val);
helper(root.right, res, level+1);
helper(root.left, res, level+1);
}
BST
98. Validate Binary Search Tree
- 考察BST的性质,从root来看,左半边子树都比root小,右半边子树都比root大,所以可以传参min和max
- DFS,双pre,在中节点处判断是否满足条件,(min和max声明为Integer类型,默认null),然后返回&&同时递归
- BFS, 标准的遍历,记录preNode,在中节点处判断root和pre的大小
235. Lowest Common Ancestor of a BST && 236. Lowest Common Ancestor of a Binary Tree
- DFS, 顺序preOrder,传参pq,中节点当判断为Null或者p或者q时,返回root;实例化左右节点递归,最后判断左右null情况返回
- Iterative, for BST, 有一种loop做法
1
2
3
4
5public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while ((root.val - p.val) * (root.val - q.val) > 0)
root = p.val < root.val ? root.left : root.right;
return root;
}
108. Convert Sorted Array to BST (binary search)
- DFS, 经典的中点建树问题,BinarySearch,传参lo, hi
109. Convert sorted List to BST
- 类比108,快慢指针找中点,每次递归找中点,结束条件是
fast != tail && fast.next != null - ++注意:递归传参是head和tail,主函数调用时tail为null++
173. BST iterator inorder
- 拆开的bfsInorder,每次call next()的时候,做一个while-pushAllLeft,popMid,toRight操作
230. Kth Smallest element in a BST (inorder)
- BFS, 标准inOrder遍历,每次处理中节点的时候count–
297. Serialize and Deserialize BST (BFS)
- 用标准的queue level order traversal。==Stack和Queue是可以存放null元素的==
- 也可以用DFS preOrder,比较快
285. Inorder Sucessor in BST
- inOrder 前后node的问题,都可以转化为BFS中节点处记录pre的问题。
270. Closest BST value (preorder)
- 利用BST的性质进行while-loop遍历,更新一个最优值
669. Trim BST
- 这种题看上去操作很复杂,其实recursive很容易就统解决了,递归返回实例化的TreeNode (root)
- preOrder DFS,先判断中节点的两种极端情况,直接剪掉一半,然后实例化分别递归
root.left和root.right,最后返回root
272. Cloest BST value II (Inorder)
- 先从上到下按性质走一遍树,双Stack记录大小node。 ++会漏掉一些node,e.g.遇到大的节点时,下一个往左走,那么node.right就漏掉了,反之亦然++
- 然后分情况操作small和large stack,先把topNode的下一个漏掉的加进去,然后用while-loop继续添加
99. Recover BST (inorder)
- 还是利用BST的性质,inOrder BST的结果是一个递增数列,e.g. 1,2,3,4,5 题中说有两个数调换了位置,所以两种情况++1. 相邻 2. 不相邻++ 1. 出现一次
pre.val > root.val2. 出现两次pre.val > root.val - 设first, second两个null,第一次更新fisrt,每次都second = root
有些题
117. Populating Next Right Pointers in Each Node II
- 类比P116的满二叉树,本题采用通式,相当于levelOrder Traversal
- while-loop循环root.next,每次设置一个cur,一个dummy,cur从左向右走,到下一层时root = dummy.next;
314. Binary Tree Vertical order Traversal
- BFS, levelOrderTraversal, root的index是0,leftNode: index-1, rightNode: index+1
- 用双Queue配合HashMap做,一个queue存node, 一个queue存index,记录min和max,mapl里每个index对应一个ArrayList
96. Unique Binary search tree (Important)
- DP问题,死记硬背,套公式:
F(n) = F(0) * F(n-1) + F(1) * F(n-2) + F(2) * F(n-3) + ... + F(n-2) * F(1) + F(n-1) * F(0)1
2
3
4//累加求DP[n]
for(int level = 2; level <= n; level++)
for(int root = 1; root <= level; root++)
dp[level] += dp[level-root]*dp[root-1];
156. Binary Tree Upside Down
- 此题为左单肩树,所有右子树都为叶子或与左子树共用父亲
- 对于最基本的左中右,upSideDown以后,
左.left=中,左.right=右,中.left=中.right=null - 可以用BFS和DFS做,参考代码-space)-and-iterative-solutions-(O(1)-space)-with-explanation-and-figure)
114. Flatten Binary Tree to Linked List (seldom)
- 实际上就是按preOrder的顺序把所有node全都弄到右边
- 因为此题要求In-Place,所以只能用DFS,建一个全局变量
preNode,注意此题在递归的时候先右后左,最后进行root的赋值操作
255. Verify Preorder Sequence in BST (Seldom)
- 此题默认也是inPlace来做,利用BST的性质,用一个stack来存node.val, 元素比top小的话就push,大的话就先把之前小的都pop出,再存大的,更新minVal,只要新val小于min就一定false
- 隐藏性质,当遇到比peek值大的元素,说明进入了当前树或者当前子树的right subTree,如果再出现比该值小的则说明false,出现更大的就进入下一个右子树或者大树的右半边树
333. Largest BST subtree (Seldom)
- Count Complete Tree Nodes (seldom)
- Construct Binary Tree From 3种order (seldom)
- Unique Binary Search Trees II (seldom)
- Verify Preorder Serialization of a Binary Tree (Seldom)